معادلات درجه دوم و اثبات روش دلتا

معادلات درجه دوم و اثبات روش دلتا

در معادله درجه دوم داریم:

$a x 2 + b x + c= 0$

با حل معادله ی فوق مقادیر x را بدست می آوریم، توجه کنید که a برابر با صفر نمی‌تواند باشد چون در این صورت معادله از نوع درجه اول می‌شود. پس با شرط a≠0 معادله را حل می کنیم :

$a(x^2+ {b \over a} x+ {c\over a}) = 0$

اگر ضرب چند عبارت برابر با صفر باشد پس حداقل یکی از آن‌ها صفر است، از آنجا که a بنا بر شرط اولیه نمی‌تواند صفر باشد پس عبارت داخل پرانتر صفر می‌باشد، پس داریم :

$x^2+ {b \over a} x+ {c\over a} = 0$

برای حل معادله آن را تبدیل به مربع کامل می کنیم :

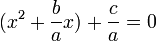
$( x^2 + {b \over a} x ) + {c \over a} = 0$

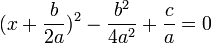
$( x + {b \over 2a} )^2 - {b^2 \over 4a^2} + {c \over a} = 0$

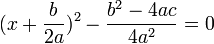
$( x + {b \over 2a} )^2 - {b^2-4ac \over 4a^2} = 0$

$( x + {b \over 2a} )^2 = {b^2-4ac \over 4a^2}$

حالا از طرفین معادله جذر می گیریم تا مقدار x را درآوریم :

$( x + {b \over 2a} ) = \pm\sqrt{b^2-4ac \over 4a^2}$

$x = \pm\sqrt{b^2-4ac \over 4a} - {b \over 2a}$

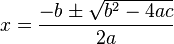
$x = {-b\pm\sqrt{b^2-4ac} \over 2 a}$

در نتیجه معادله دارای 2 ریشهٔ زیر می‌باشد:

$x_1 = {-b + \sqrt{b^2-4ac} \over 2 a}$

$x_2 = {-b - \sqrt{b^2-4ac} \over 2 a}$

با توجه به اینکه عبارت $\sqrt{b^2-4ac}$ برابر دلتا می باشد. به این عبارت میرسیم:

$x = {-b\pm\sqrt{\Delta} \over 2 a}$

و میبینیم که این روش اثبات شد!

با تشکر که با ما بودید!! موفق باشید!

+ نوشته شده در چهارشنبه بیست و چهارم فروردین ۱۳۹۰ ساعت 22:48 توسط سید حسن |